并行計算中的BSP模型

牽牛吃草 2018-08-29

展開全文

計算模型

所謂計算模型實際上就是硬件和軟件之間的一種橋梁,，我們可以借助它來設計分析算法,，在其上髙級語言能被有效地編譯且能夠用硬件來實現(xiàn)。在串行計算時,，馮·諾依曼機就是一個理想的串行計算模型,，在此模型上硬件設計者可設計多種多樣的馮·諾依曼機而無須考慮那些將要被執(zhí)行的軟件；另一方面,，軟件工程師也能夠編寫各種可在此模型上有效執(zhí)行的程序而無須考慮所使用的硬件,。

不幸的是,，在并行計算時，尚未有一個類似于馮·諾依曼機的真正通用的并行計算模型?，F(xiàn)在流行的計算模型要么過于簡單,、抽象（如PRAM）；要么過于專用（如互連網絡模型和VLSI計算模型）,。因而急需發(fā)展一種更為實用,、能夠較真實反映現(xiàn)代并行機性能的并行計算模型。我們在之前的文章中已經討論過PRAM模型,。讀者可以參考我的博客文章《PRAM模型與Amdahl定律》

簡而言之,，PRAM模型，即并行隨機存取機器,，也稱之為共享存儲的SIMD模型,，是一種抽象的并行計算模型。在這種模型中,，假定存在著一個容量無限大的共享存儲器,；同時存在有限（或無限）個功能相同的處理器，且其均具有簡單的算術運算和邏輯判斷功能,；在任何時刻各處理器均可通過共享存儲單元相互交換數(shù)據(jù),。根據(jù)處理器對共享存儲單元是否可以同時讀、同時寫的限制,， PRAM模型又可分為：EREW,、CREW、CRCW等幾種類型,。

下面本文將介紹另外一種并行計算模型——BSP模型,。

BSP模型

BSP（Bulk Synchronous Parallel）模型，字面的含義是 “大”同步模型,，它最早由Leslie和Valiant 在 1990 年提出,。作為計算機語言和體系結構之間的橋梁，BSP使用下面三個參數(shù)（或屬性）來描述的分布存儲的多處理器模型：

處理器/儲器模塊: A BSP abstract machine consists of a collection of p abstract processors, each with local memory, connected by an interconnection network.
執(zhí)行以時間間隔L為周期的所謂路障同步器：the time to do a barrier synchronization.
施行處理器/儲器模塊對之間點到點傳遞消息的選路器: the rate at which continuous randomly addressed data can be delivered

所以BSP模型將并行機的特性抽象為三個定量參數(shù)p,、g,、L,分別對應于處理器數(shù)、選路器吞吐率(亦稱帶寬因子）,、全局同步之間的時間間隔,。

BSP模型中的計算行為：在BSP模型中，計算過程是由一系列用全局同步分開的周期為L的超級步（supersteps)所組成的,。A (abstract) program consists of $p$ processes or threads distributed over $n$ processors and is divided into supersteps,。在各superstep中,，每個處理器均執(zhí)行局部計算,，并通過選路器接收和發(fā)送消息,；然后做一全局檢查，以確定該超級步是否已由所有的處理器完成：若是,，則前進到下一超級步,，否則下一個 $L$ 周期被分配給未曾完成的超級步。
每個superstep都包含：

a computation where each processor (executing the threads assigned to it) uses only locally held values;
a global message transmission from each processor to any subset of the others;
a barrier synchronization.

在superstep結束時,，the transmitted messages become available as
local data for the next superstep,。下圖是BSP里一個superstep中的計算模式示意圖：

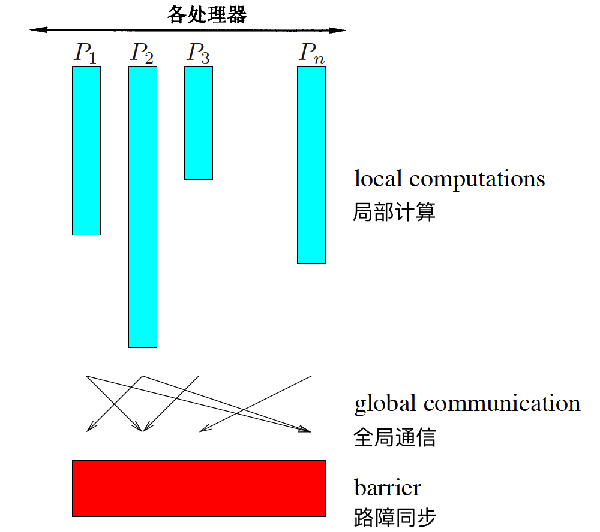
BSP模型的性質和特點：BSP模型是個分布存儲的MIMD計算模型，其特點是:

它將處理器和選路器分開,，強調了計算任務和通信任務的分開,，而選路器僅施行點到點的消息傳遞，不提供組合,、復制或廣播等功能,，這樣做既掩蓋了具體的互連網絡拓撲，又簡化了通信協(xié)議; With the program divided into supersteps it is easier to provide performance guarantees than with unregulated message-passing systems. Because communication all happens together at the end of the computation phase of the superstep, it is possible to perform automatic optimisation of the communications pattern. This is particularly important on machines where the start-up cost of a communication is high: if during a superstep processor i sends two messages to processor j , then it will often be quicker to bundle the messages together and send the bundle from
i to j than it would be to send each message separately. Similarly, the communication pattern can be reshuffled to avoid network congestion, and intelligent routing techniques can be used to detect and avoid hot spots,。
釆用路障方式的以硬件實現(xiàn)的全局步是在可控的粗粒度級,，從而提供了執(zhí)行緊耦合同步式并行算法的有效方式，而編程開發(fā)人員并無過分的負擔,，BSP model eliminates the need for programmers to manage memory, assign communication and perform low-level synchronization. Threads of the program are assigned (typically in a randomized way) by the machine to the processors.;
在分析BSP模型的性能時,，假定局部操作可在一個時間步內完成，而在每一個superstep中,，一個處理器至多發(fā)送或接收 h 條消息（稱為h-relation),。假定 $s$ 是傳輸建立時間，所以傳送 h 條消息的時間為 gh+s,，如果 $g h \geq 2 s$ ,，則 L 至少應 $\geq g h$ 。很清楚,，硬件可將L設置盡量小(例如使用流水線或寬的通信帶寬使 g盡量?。浖梢栽O置L之上限（因為L愈大,，并行粒度愈大）,。在實際使用中，g可定義為每秒處理器所能完成的局部計算數(shù)目與每秒選路器所能傳輸?shù)臄?shù)據(jù)量之比,。如果能合適地平衡計算和通信,，則BSP模型在可編程性方面具有主要的優(yōu)點，它可直接在BSP模型上執(zhí)行算法（不是自動地編譯它們）,，此優(yōu)點將隨著g 的增加而更加明顯;
為PRAM模型所設計的算法,，均可釆用在每個BSP處理器上模擬一些PRAM處理器的方法實現(xiàn)之。This leads to optimal efficiency (i.e., within a constant factor performance of the PRAM model) provided the programmer writes programs with sufficient parallel slackness,。理論分析證明,，這種模擬在常數(shù)因子范圍內是最佳的,，只要并行寬松度（Parallel Slackness)，即每個BSP處理器所能模擬的PRAM處理器的數(shù)目足夠大（When programs written for p threads are run on n processors and p >> n (e.g. p = n log n) then there is some parallel slackness）,。在并發(fā)情況下,，多個處理器同時訪問分布式的存儲器會引起一些問題，但使用散列方法可使程序均勻地訪問分布式存儲器,。在 PRAM-EREW情況下,，如果所選用的散列函數(shù)足夠有效，則 $L$ 至少是對數(shù)的,，于是模擬可達最佳,，這是因為我們欲在擁有 $p$ 個物理處理器的BSP模型上，模擬 $v \geq p \log p$ 個虛擬處理器,，可將 $v / p \geq \log p$ 個虛擬處理器分配給每個物理處理器,。在一個supersetp內， $v$ 次存取請求可均勻攤開,，每個處理器大約 $v / p$ 次,，因此機器執(zhí)行本次超級步的最佳時間為 $O (v / p)$ ，且概率是高的,。同祥,，在 $v$ 個處理器的 PRAM-CRCW模型中，能夠在 $p$ 個處理器（如果 $v = p^{1 + ϵ}, ϵ > 0$ ）和 $L \geq \log p$ 的BSP模型上用 $O (v / p)$ 的時間也可達到最佳模擬,。